Erlang C Formula – Made Simple With an Easy Worked Example

The Erlang C formula is quite complex to look at, but can be straightforward to apply, if you follow these easy steps.

We have also included a worked example in Excel to help you follow the maths.

But before we dive into the maths, here is some key information about the Erlang C formula and its derivation:

What Is the Erlang C Formula?

The Erlang C formula is a mathematical equation for calculating the number of agents (advisors) that you need in a call centre, given the number of calls and the service level that you want to achieve.

The Erlang C formula is the most important part of the equation. It allows you to work out the probability that a call waits (P_w), given the Traffic Intensity (A) and the Number of Agents (N) available.

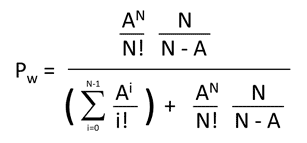
It was named after the Danish Mathematician A.K. Erlang, who developed the Erlang C formula 100 years ago in 1917.

A.K. Erlang published (in Danish) his landmark paper “Solution of some problems in the theory of probabilities of significance in automatic telephone exchanges,”  In the Journal Electroteknikeren 13: 5–13 (1917)

It first appeared in English in the Post Office Electrical Engineers Journal Volume 10 (1917–1918) Pages 189–197

It is a derivation of the Poisson Formula – but using a special case where k=0.  This assumes that the Average Handling Time of calls is distributed by a version of Poisson called the Erlang Distribution.

For more information on this topic, read our article: How Is Average Handling Time Distributed? It Is Not How You Think!

Why Should You Use Erlang C?

As a call centre manager, if you want to save costs and improve your customer experience (CX), you should understand Erlang C and how to use it.

Why? By understanding the principles behind Erlang C, call centre managers can better:

• Understand call load and call distribution
• Understand service level
• Manage costs
• Create a more stable user experience

After all, you don’t want too many agents to be scheduled when there are only a few calls.

A Step by Step Guide to the Erlang C Formula

1. The Inputs

Before we start, we need a number of inputs.

We will use a worked example of 100 calls per half hour, with an Average Handling Time of 3 minutes. I have chosen this example as it uses nice round numbers in the maths.  

2. Work Out the Number of Calls Per Hour

So, we have 100 calls per 30 minutes, which works out as 200 calls per hour

3. Work Out the Traffic Intensity (A)

The traffic intensity is the length of time that all of the phone calls would take if ordered end to end.

So if we have 200 calls with an Average Handling Time of 3 minutes, we would have a total of 200 x 3 = 600 call minutes.

To work out the traffic intensity, take the call minutes and divide by 60 to get the number of call hours.

So, 600 call minutes / 60 = 10 Call Hours.

Now the technical unit for Call Hours is called an Erlang.

So the traffic intensity = 10 Call Hours = 10 Erlangs.

4. Estimate the Raw Number of Agents Required (N)

We now need to estimate the Raw Number of Agents Required to handle this traffic intensity.

We know that we have 10 Erlangs (10 calls hours of traffic per hour). This means that the minimum number of agents that we would need in the call centre would be 10 agents.

This figure of 10 agents would assume that all calls arrive at exactly the moment that a previous call has finished and that there is no queuing.

So, we start with adding 1 to the traffic intensity.

Estimate 1: N = A + 1 = 10 + 1 = 11 Agents

We then feed the Traffic Intensity (A) and the Number of Agents (N) into the Erlang C formula to see what is the probability that a call waits and then work out the Service Level.

We then increase the Number of Agents until Service Level is met.

5. Calculate the Erlang Formula for Probability a Call Waits

Here is the formula from Wikipedia:

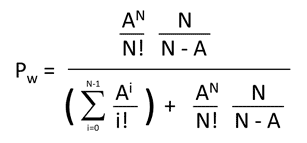
You may also see it written like this.

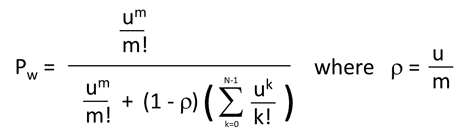
Don’t worry; this is the same formula. It just uses different units (u) and (m) and has a factor multiplied across the top and the bottom of the formula.  (If you are uncertain, scroll down to the bottom of the page where I will show how they are the same formula.)

This looks scary so let’s look at the key elements individually and build it up in stages.

6.  Work Out N! (N Factorial)

N! is mathematical notation for N factorial.

So you need to cast your mind back to school maths. A factorial is the product of an integer (whole number) and all the integers (whole numbers) below it.

For example    3! = 3 Factorial = 3 x 2 x 1 = 6

So N! = 11! = 11 Factorial = 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 39916800

For reference, here is a lookup table of the first 20 Factorials.  We will need this for the worked example.

Luckily, Excel has a formula that can do this for you.

So, for 11 Factorial it is =FACT(11)

N! = 11! = 11 Factorial = FACT (11) = 39916800

7. Be Careful With Large Factorials

Note that factorials get very large as you increase the number of agents and very soon can cause Excel (and some computer languages) to overload, as highlighted below.

10! = 10 Factorial = FACT(10) = 3628800
100! = 100 Factorial = FACT(100) = 9.3326 x 10¹⁵⁷
170! = 170 Factorial = FACT(170) = 7.2574 x 10³⁰⁶
171! = 171 Factorial = FACT(171) = #NUM!

The #NUM! shows that Excel is overloaded and can give you erroneous answers.

On some Erlang Calculators you will see this Error written as NaN (Not a Number).

So it won’t easily work in Excel above 170 agents.

Luckily, we have devised a Fast Erlang formula for a high number of agents as part of our Erlang Calculator

8. Work Out the Powers – A^N

So, A^N means A multiplied by A, N times.

For example: 2 to the power of 2 = 2² = 2 x 2 = 4

So if A = 10 and N = 11, then A^N = 10¹¹ = 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10 x 10

Luckily, Excel has a formula for this = POWER (10,11)

A^N = 10¹¹ = POWER (10,11) = 1 x 10¹¹

9. Let’s Simplify the Erlang C Formula

We can use a substitution, to substitute X and Y  for the complex parts of the equation: P_w = X / ( Y + X)

10. Let’s Work Out the Top Row of the Erlang Formula (X)

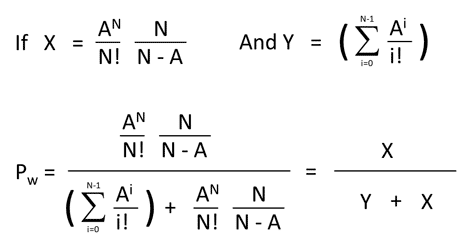
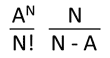
X = A^N / N! * [N / (N-A)]

X = 10¹¹ / 11! * [11 / (11-10)]

X = 10¹¹ / 11! * (11 / 1)

X = 10¹¹ / 11! * 11

X = 27557.32

11. Work Out the Sum of a Series (Y)

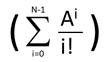
Now this looks scary, but it is simply adding together a sum of Aⁱ / i! from zero to a maximum value of N-1.

In this case, you start with i=0 and keep going through until i= N-1

So, if N = 11 , N – 1 = 10 and we loop through from i= 0 until i = 10, as shown below.

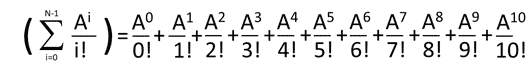
Σ is the mathematical symbol for the sum of a series, so you add together all of the results of the individual loops.

This means that the sum of the series Y = 12842.3

12. Put X and Y into the Erlang C Formula (The probability a call has to wait)

So P_w = X / ( Y + X)

P_w = 27557 / (12842 + 27557) = 0.6821

Or in percentage terms 68.2%

13. Calculate the Service Level

Service Level follows the formula:

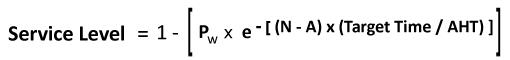
Where e is the mathematical constant (Euler’s number)  and will always equal 2.71828.

Luckily, Excel has an equation for this =EXP()

Let’s work out -(N – A) * (TargetTime / AHT)

Let’s work out -(11 – 10) * (20 /180) = -0.111

Then work out Service Level

SL = 1- (0.6821 * EXP(-0.11111)) = 0.390

Service Level as a Percentage = 39.0%

This is below the target of 80%, so we need to increase the number of agents.

14. Increase the Number of Agents (N) by 1 to See if Service Level Is Achieved

We keep on increasing the Number of Agents (N) by 1 to see if Service Level is achieved. We keep looping through steps 4 to 12 until we meet service level.

This can be done by hand but can be a bit tedious.

For the sake of completeness, I have included the calculations below:

14.1 Number of Agents N = 12

Traffic Intensity A = 10

Work out X = 12526.1

Work out Y = 15347.5

Probability Call Waits = 0.4494

Service Level = 0.640

Service Level as a Percentage 64.0%. This is below the target of 80% so we need to increase the number of agents.

14.2.  Increase the Number of Agents by 1 to See if Service Level Is Achieved

Number of Agents  N = 13

Traffic Intensity A = 10

Work out X = 6958.9

So value of Y = 17435.2

Probability Call Waits 0.2853

Service Level 0.796

Service Level as a Percentage 79.6%

This is below the target of 80% so we need to increase the number of agents

14.3.  Increase the Number of Agents by 1 to See if Service Level Is Achieved

Number of Agents = N 14

Traffic Intensity = A 10

Work out X = 4014.8

So the value of Y = 19041.1

Probability Call Waits = 0.1741

Service Level = 0.888

Service Level as a Percentage = 88.8%

This is above the target of 80%

So the Raw Number of Agents = 14

(Please note that this does not include Shrinkage or Maximum Occupancy)

15.  Average Speed of Answer (ASA)

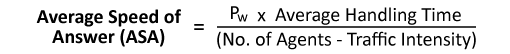
ASA = 0.1741 x 180 / (14 – 10) = 7.8 seconds

16. Percentage of Calls Answered Immediately

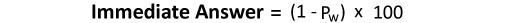
Immediate Answer = (1- 0.1741) = 0.826 = 82.6%

17. Check Maximum Occupancy

Occupancy is the percentage of time that all call centre agents spend handling customer contacts. The formula is shown below.

Raw Agents = 14

Traffic Intensity A = 10

Occupancy = (10 / 14) x 100 = 71.4%

This is less than 85% so we can keep it at this.

If this is more than 85%, the number of Raw Agents = Traffic Intensity/ (Occupancy %/100)

If you have an occupancy of more than 85%, your agents will likely get burnt out and you will find that Average Handling Time (AHT) may rise to cover it.

18. Factor In Shrinkage

Shrinkage is a factor that is widely used in the industry to include holidays, sickness, training and meetings etc. The industry average is around 30–35%

Shrinkage = 30%

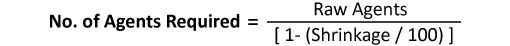
Number of Agents Required = 14/ 0.7 = 20

To find out your contact centre’s shrinkage rate, read our article: How to Calculate Contact Centre Shrinkage

19. Summary

So the total number of Agents Required – 20

Service Level – 88.8%

Probability a call has to wait – 17.4%

Average Speed of Answer – 7.8 Seconds

% of calls Answered Immediately – 82.6%

20.  There Is an Easier (and Faster) Way to Do an Erlang C Calculation

There is a much easier (and faster) way to use the Erlang C Formula.

We have developed two Erlang Calculators

• Erlang Calculator (Online Version)
• Excel Erlang Calculator (Handy spreadsheet format)

The added advantage of these calculators is that we have already figured out how to increase the calculations above the limit of 172 Agents and they are accurate to 10,000 Agents for the online Version and 600 Agents for the Excel Version.

Also, if you want a spreadsheet that explains the Erlang C Formula you can download it here.

Proof That the Two Versions of the Erlang C Formula Are the Same

Here is the Wikipedia Version.

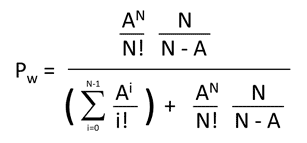
Here is the other version.

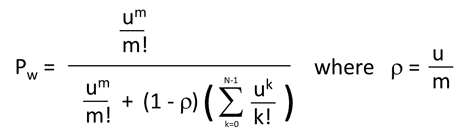
Let’s substitute ρ= u/m.

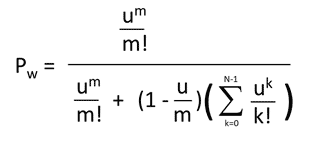
Now since u is traffic intensity (A), and m is the number of agents (n) we can substitute the equation.

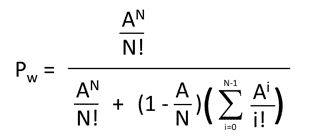
We can write the numerators and denominators of part of the equation in a different way.

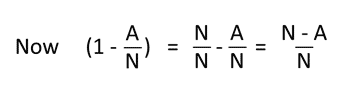
Let’s divide the top half and the bottom half of the equation by (N-A) /N

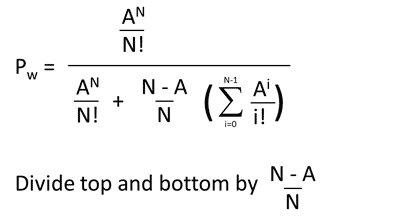
Which produces

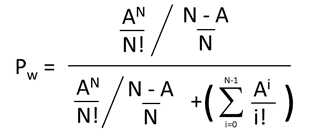
Now since dividing by a/b is the same as multiplying by b/a, dividing by (N-A)/N is the same as multiplying by N/(N-A).

Which gives

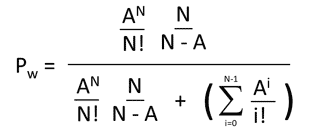
And since X + Y is the same as Y + X we can express it as

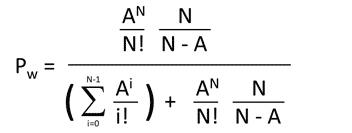
Which is our original Erlang C formula.

Find out more about the other Erlang equations and functions in our articles:

• A Beginner’s Guide to the Erlang A Formula
• What Is an Erlang Calculator?
• What are Erlangs?

Reviewed by: Xander Freeman